ロボットの手先位置を現在位置から目標位置へ移動させるには、各関節角度から手先位置をもとめる順運動学と手先位置から各関節角度を求める逆運動学を用いる必要があります。手先位置を前方に100mm、右に200mm、上に300mm移動させるときに、各関節の位置をどのように動かさないといけないか計算しなければなりません。そのときに、順運動学と逆運動学を使います。ここでは順運動学について説明します。
デバビット・ハーテンバーグの記法
ロボットの各関節の相対位置関係から手先の位置姿勢を求めます。その相対位置関係を定義する方法として、Denavit-Hartenbergの記法があります。
下図のように各関節の座標を定義したとします。
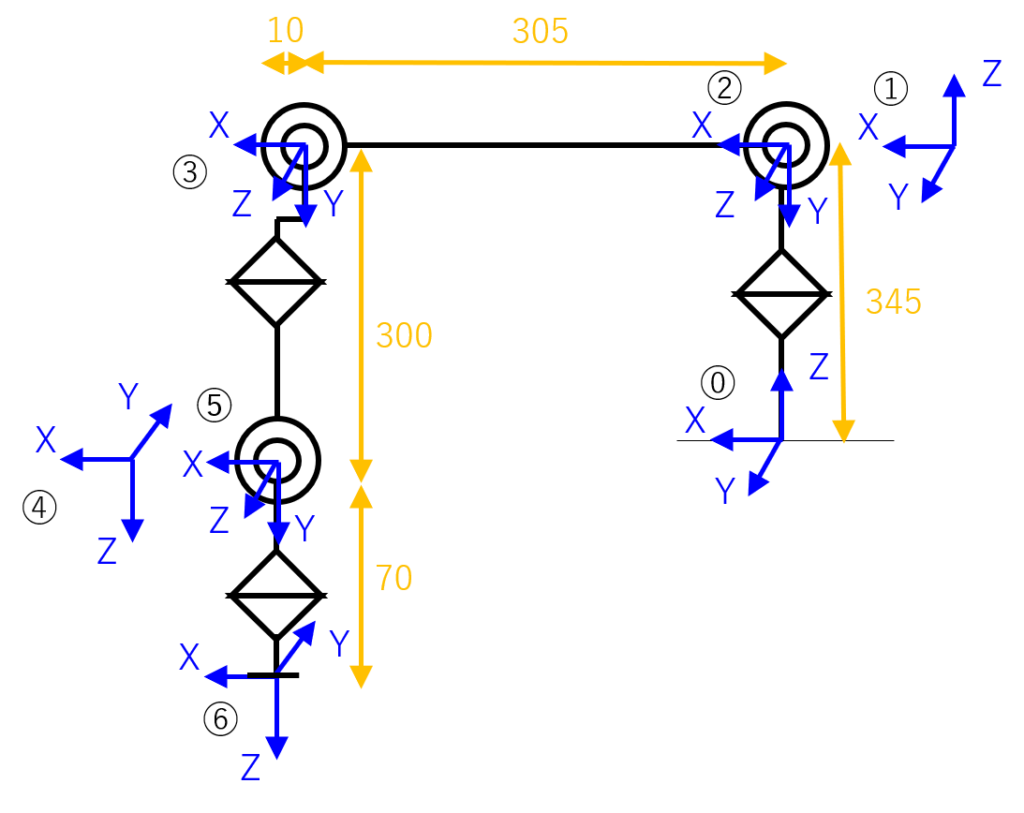
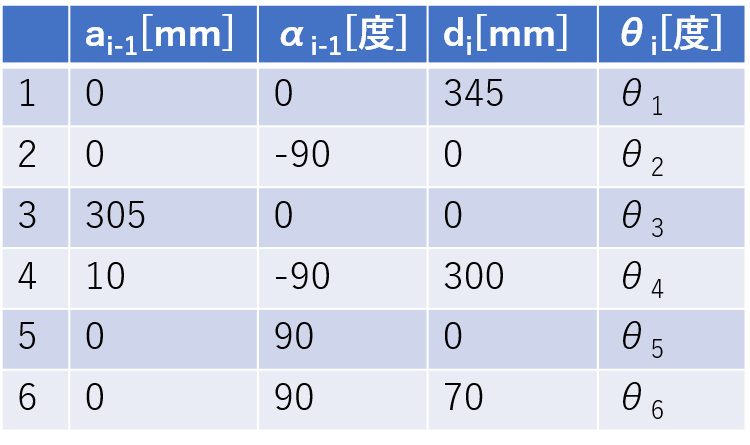
Denavit-Hartenbergの記法では、下の表で表されます。1は⓪⇒①、2は①⇒②、3は②⇒③、4は③⇒④、5は④⇒➄、6は➄⇒⑥の座標の相対位置関係を示します。aはX軸方向の距離、αはX軸回りの回転角度、dはZ軸方向の距離、θはZ軸回りの回転角度になります。なお、dとθは、αでX軸回りに回転した後のZ軸を基準となります。
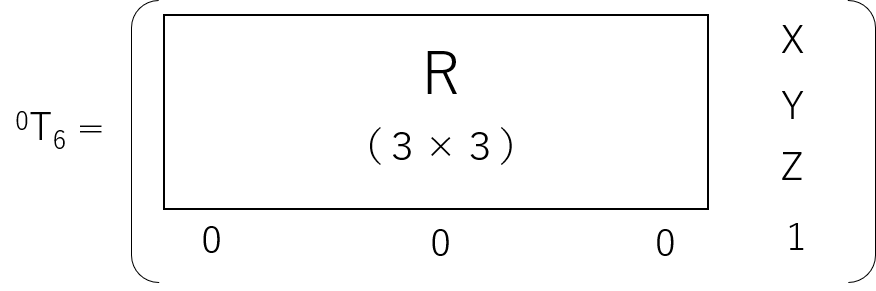
同次変換行列
同次変換行列とは、相対位置姿勢を示す行列です。例えば、0T1は、⓪⇒①の同次変換行列を示します。X軸方向にa移動、α回転し、Z軸方向にd移動、θ回転した場合の同次変換行列は、4×4の行列で以下の式になります。

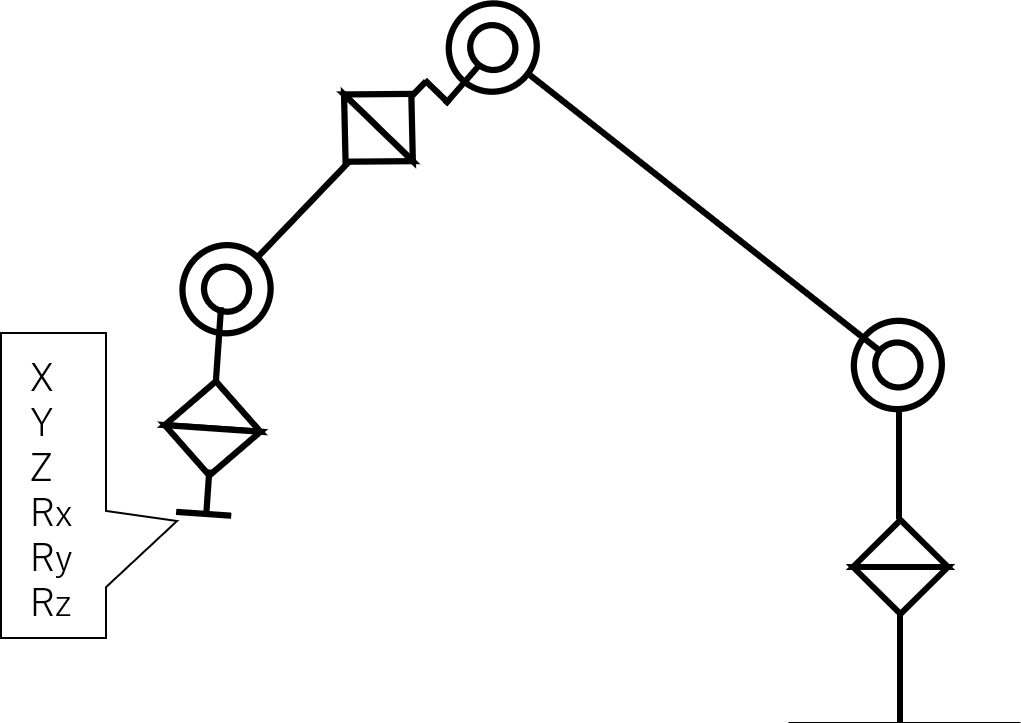
0T6=0T11T22T33T44T55T6のように6軸分掛け合わせると、ベースの座標基準のロボット先端の位置姿勢が求められます。下記のように0T6の右上3つがX,Y,Zの位置を示し、左上の3×3の行列Rが姿勢を示します。行列Rは、回転行列と呼ばれ、姿勢角Rx,Ry,Rzに変換することができます。
各関節角度のθ1~θ6が決まると、0T6が求まり、ロボット手先の位置姿勢のX[mm],Y[mm],Z[mm],Rx[度],Ry[度],Rz[度]が計算できます。これらは、⓪を基準とした位置姿勢です。行列計算や姿勢角については別途説明します。


コメント